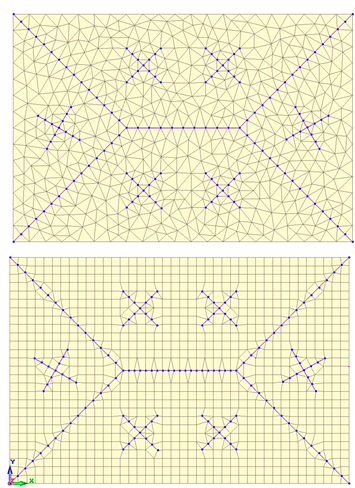
Триангуляция. Построение конечноэлементных сеток
Построение конечно элементных сеток является важным этапом решения задачи по определению НДС конструкций. Этот этап связан с удовлетворением ряда противоречивых требований.
ПК ЛИРА-САПР идеально подходит для расчета по методу конечных элементов. В программе представлена обширная библиотека конечных элементов.
ПК ЛИРА-САПР это программа для расчета конструкций по методу конечных элементов (МКЭ). В программном комплексе ЛИРА-САПР метод конечных элементов реализован в форме перемещений – МКЭ рассматривается для случаев, когда искомой разрешающей функцией служит перемещение. Это вызвано тем, что выбор расчетной схемы для МКЭ в перемещениях легко поддается алгоритмизации, а практическое использование МКЭ немыслимо без применения современных компьютеров.
Метод конечных элементов основан на мысленном представлении сплошного тела в виде совокупности отдельных конечных элементов, взаимодействующих между собой в конечном числе точек, которые в МКЭ принято называть узлами.
Расчет строительных конструкций с использованием метода конечных элементов (МКЭ) являет собой представление упругих систем в виде набора элементов с конечным числом степеней свободы, которые соединяются между собой в узловых точках (узлах). Такое представление заданной системы приводит к полной формализации всех этапов расчета. Подход к решению задачи является единым, как для стержневых систем, так и для пластин, оболочек, объемных тел и т.п.
Библиотека конечных элементов (БКЭ) содержит элементы, моделирующие работу различных типов конструкций: элементы стержней, четырехугольные и треугольные элементы плоской задачи, плиты, оболочки, элементы пространственной задачи – тетраэдр, параллелепипед, трехгранная призма. Кроме того, в БКЭ имеются различные специальные элементы, моделирующие связь конечной жесткости, упругую податливость между узлами, элементы, задаваемые численной матрицей жесткости.
В скобках указан признак схемы, где допускается использование КЭ данного типа.
Тип 1. Стержневой КЭ плоской фермы (1,2,5)
Тип 2. Стержневой КЭ плоской рамы (2,5)
Тип 3. Стержневой КЭ балочного ростверка (3,5)
Тип 4. Стержневой КЭ пространственной фермы (4,5)
Тип 7. Пространственный стержневой тонкостенный КЭ с учетом депланации сечения (6)
Тип 10. Универсальный пространственный стержневой КЭ (1,2,3,4,5,6)
Тип 11. Прямоугольный КЭ плиты (3,5)
Тип 12. Треугольный КЭ плиты (3,5)
Тип 15. Универсальный прямоугольный КЭ толстой плиты (3,5)
Тип 16. Универсальный треугольный КЭ толстой плиты (3,5)
Тип 17. Универсальный четырехугольный КЭ толстой плиты (3,5)
Тип 19. Четырехугольный КЭ плиты (3,5)
Тип 21. Прямоугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 22. Треугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 23. Универсальный прямоугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 24. Универсальный треугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 27. Универсальный четырехугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 30. Четырехугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 31. Параллелепипед (4,5)
Тип 32. Тетраэдр (4,5)
Тип 33. Прямая треугольная призма (4,5)
Тип 34. Пространственный шестиузловой изопараметрический КЭ (4,5)
Тип 36. Пространственный восьмиузловой изопараметрический КЭ (4,5)
Тип 41. Универсальный прямоугольный КЭ оболочки (5)
Тип 42. Универсальный треугольный КЭ оболочки (5)
Тип 44. Универсальный четырехугольный КЭ оболочки (5)
Тип 45. Универсальный прямоугольный КЭ толстой оболочки (5)
Тип 46. Универсальный треугольный КЭ толстой оболочки (5)/p>
Тип 47. Универсальный четырехугольный КЭ толстой оболочки (5)
Тип 51. Одноузловой КЭ упругой связи (1,2,3,4,5)
Тип 52. КЭ задаваемый численной матрицей жесткости. Конечный элемент, задаваемый численной матрицей жесткости. Применяется для отладки новых типов конечных элементов.
Тип 53. Законтурный двухузловой КЭ упругого основания (3,4,5)
Тип 54. Законтурный одноузловой КЭ упругого основания (3,4,5)
Тип 55. Двухузловой КЭ упругих связей между узлами (1,2,3,4,5)
Тип 56. Одноузловой КЭ упругих связей (1,2,3,4,5)
Тип 57. Одноузловой КЭ одиночной сваи (1,2,3,4,5)
Тип 58. Треугольный КЭ стыка (5)
Тип 59. Четырехугольный КЭ стыка (5)
Тип 60. Двухузловой КЭ многослойного упругого основания (1,2,3,4,5)
Тип 62. Двухузловой КЭ вязкого демпфирования (1,2,3,4,5)
Тип 67. Двухузловой КЭ для моделирования плоского безграничного грунтового массива (1,2,3,4,5)
Тип 68. Треугольный КЭ для моделирования пространственного безграничного грунтового массива (4,5)
Тип 69. Четырехугольный КЭ для моделирования пространственного безграничного грунтового массива (4,5)
Тип 82. Треугольный КЭ плоской задачи (массив) (1,2,5)
Тип 84. Четырехугольный КЭ плоской задачи (массив) (1,2,5)
Тип 201. Физически нелинейный стержневой КЭ плоской фермы (1,2,5)
Тип 202. Физически нелинейный стержневой КЭ плоской рамы (2,5)
Тип 204. Физически нелинейный стержневой КЭ пространственной фермы (4,5)
Тип 207. Физически нелинейный двухузловой КЭ предварительного обжатия (домкрат) (1,2,4,5)
Тип 208. Физически нелинейный двухузловой КЭ предварительного натяжения (1,2,4,5)
Тип 210. Физически нелинейный универсальный пространственный стержневой КЭ (1,2,3,4,5)
Тип 221. Физически нелинейный прямоугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 222. Физически нелинейный треугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 223. Физически нелинейный универсальный прямоугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 224. Физически нелинейный универсальный треугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 227. Физически нелинейный универсальный четырехугольный КЭ плоской задачи (балка-стенка) (4,5)
Тип 230. Физически нелинейный четырехугольный КЭ плоской задачи (балка-стенка) (1,2,5)
Тип 231. Физически нелинейный параллелепипед (4,5)
Тип 232. Физически нелинейный тетраэдр (4,5)
Тип 233. Физически нелинейная прямая треугольная призма (4,5)
Тип 234. Физически нелинейный пространственный шестиузловой изопараметрический КЭ (4,5)
Тип 236. Физически нелинейный пространственный восьмиузловой изопараметрический КЭ (4,5)
Тип 241. Физически нелинейный универсальный прямоугольный КЭ оболочки (5)
Тип 242. Физически нелинейный универсальный треугольный КЭ оболочки (5)
Тип 244. Физически нелинейный универсальный четырехугольный КЭ оболочки (5)
Тип 245. Физически нелинейный прямоугольный КЭ толстой оболочки (5)
Тип 246. Физически нелинейный треугольный КЭ толстой оболочки (5)
Тип 247. Физически нелинейный четырехугольный КЭ толстой оболочки (5)
Тип 251. Одноузловой КЭ односторонней связи с учетом предельного усилия (односторонний аналог КЭ 51 с учетом предельного усилия) (1,2,3,4,5)
Тип 252. Двухузловой КЭ односторонней связи с учетом предельного усилия (1,2,3,4,5)
Тип 255. Двухузловой КЭ упругих связей с учетом предельных усилий (аналог КЭ 55 с учетом предельных усилий) (1,2,4,5)
Тип 256. Одноузловой КЭ упругих связей с учетом предельных усилий (аналог КЭ 56 с учетом предельных усилий) (1,2,3,4,5)
Тип 258. Треугольный КЭ стыка с учетом нелинейной работы (аналог КЭ 58 с учетом нелинейной работы) (5)
Тип 259. Четырехугольный КЭ стыка с учетом нелинейной работы (аналог КЭ 59 с учетом нелинейной работы) (5)
Тип 261. Одноузловой КЭ односторонней упругой связи (1,2,3,4,5)
Тип 262. Двухузловой КЭ односторонней упругой связи между узлами (1,2,3,4,5)
Тип 263. Одноузловой КЭ односторонней упругой связи с трением (1,2,4,5)
Тип 264. Двухузловой КЭ односторонней упругой связи с трением между узлами (1,2,4,5)
Тип 265. Двухузловой КЭ односторонних упругих связей (аналог КЭ 55 с учетом односторонней работы) (1,2,4,5)
Тип 266. Одноузловой КЭ односторонних упругих связей (аналог КЭ 56 с учетом односторонней работы) (1,2,3,4,5)
Тип 271. Физически нелинейный параллелепипед (грунт) (4,5)
Тип 272. Физически нелинейный тетраэдр (грунт) (4,5)
Тип 273. Физически нелинейная прямая треугольная призма (грунт) (4,5)
Тип 274. Физически нелинейный пространственный шестиузловой изопараметрический КЭ (грунт) (4,5)
Тип 276. Физически нелинейный пространственный восьмиузловой изопараметрический КЭ (грунт) (4,5)
Тип 281. Физически нелинейный прямоугольный КЭ плоской задачи (грунт) (1,2,5)
Тип 282. Физически нелинейный треугольный КЭ плоской задачи (грунт) (1,2,5)
Тип 284. Физически нелинейный четырехугольный КЭ плоской задачи (грунт) (1,2,5)
Тип 295. Двухузловой КЭ нелинейных упругих связей (аналог КЭ 255 с учетом нелинейной работы) (1,2,4,5)
Тип 296. Одноузловой КЭ нелинейных упругих связей (аналог КЭ 256 с учетом нелинейной работы) (1,2,3,4,5)
Тип 308. Геометрически нелинейный двухузловой КЭ для моделирования предварительного натяжения (1,2,4,5)
Тип 309. Геометрически нелинейный универсальный пространственный сильно изгибаемый стержневой КЭ (1,2,3,4,5)
Тип 310. Геометрически нелинейный универсальный пространственный стержневой КЭ (нить) (1,2,3,4,5)
Тип 341. Геометрически нелинейный прямоугольный КЭ оболочки (5)
Тип 342. Геометрически нелинейный треугольный КЭ оболочки (5)
Тип 344. Геометрически нелинейный четырехугольный КЭ оболочки (5)
Тип 410. Универсальный пространственный стержневой КЭ с учетом физической и геометрической нелинейности (1,2,3,4,5)
Тип 441. Прямоугольный КЭ оболочки с учетом физической и геометрической нелинейности (5)
Тип 442. Треугольный КЭ оболочки с учетом физической и геометрической нелинейности (5)
Тип 444. Четырехугольный КЭ оболочки с учетом физической и геометрической нелинейности (5)
Тип 1505. Стержневой КЭ теплопроводности (15)
Тип 1508. Треугольный КЭ теплопроводности (15)
Тип 1509. Четырехугольный КЭ теплопроводности (15)
Тип 1512. КЭ теплопроводности в форме тетраэдра (15)
Тип 1514. Объемный шестиузловой КЭ теплопроводности (15)
Тип 1516. Объемный восьмиузловой КЭ теплопроводности (15)
Тип 1551. Одноузловой КЭ конвективного теплообмена (15)
Тип 1555. Двухузловой КЭ конвективного теплообмена (15)
Тип 1558. Треугольный КЭ конвективного теплообмена (15)
Тип 1559. Четырехугольный КЭ конвективного теплообмена (15)
ПК ЛИРА-САПР имеет свидетельство о верификации РААСН.
Особое внимание мы уделяем точности и достоверности полученных результатов расчета. Поэтому реализация новых возможностей требует от нас тщательной проверки результатов, в сравнении с раннее известными аналитическими решениями данного класса задач, а также в сравнении результатов с другим программным обеспечением, которое используется для решения инженерных задач.


Если у вас все еще есть сомнения, загрузите демонстрационную версию и попробуйте или свяжитесь с нашей службой поддержки для получения более подробной информации.